= Μα καλά, γιατί όλη αυτή η φασαρία;
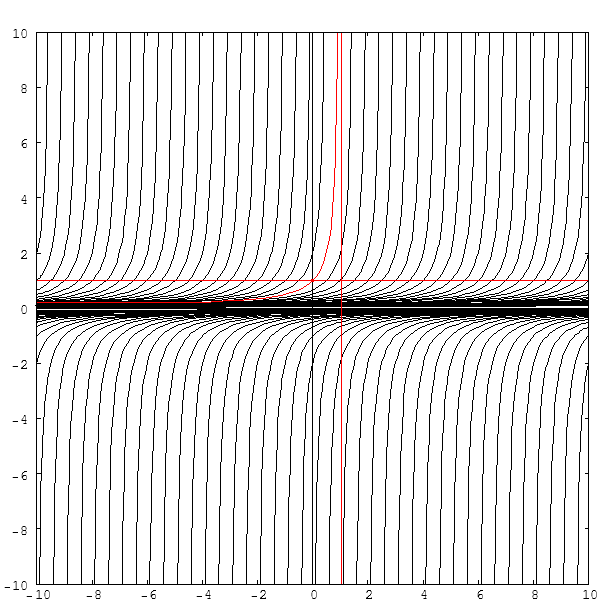
- Χμ! Για να διερευνηθεί ή αλήθεια του εξής "προκλητικού" ισχυρισμού για τη δεύτερη ΔΕ (p. 13, op. cit.) : "Thus if x0 = 0, y0 = 1 are the initial conditions, y = 1/(1 - x) which has only a finite range in which it is continuous ...", όταν έχουμε ήδη διαπιστώσει πως η ειδική λύση με την ίδια αρχική συνθήκη (x0 = 0, y0 = 1) της πρώτης ΔΕ έχει -και στις δύο περιπτώσεις "αρχικής" τιμής, γενικώς και κυριολεκτικώς- μέγιστο διάστημα ορισμού που είναι (ημι-)άπειρο (δεξιά) -ίσο προς (-1, +οο) και [0, +οο) αντιστοίχως. Τι παρατηρούμε όμως από την παραπάνω ζωγραφιά; Ότι με την μεν γενική έννοια της αρχικής συνθήκης το εν λόγω διάστημα ορισμού είναι το (αριστερά ημι-) άπειρο (-οο, 1), υπερδιάστημα δηλαδή εκείνου της κυριολεκτικής αρχικής συνθήκης που είναι "μόνον" το υποδιάστημά του [0, 1) . Αυτό όμως είναι πεπερασμένο (περιορισμένο). Όθεν, ορθός ο εν λόγω ισχυρισμός! - d;^) -
- Με την ευκαιρία, αφού επαναλάβουμε την διαπίστωση πως τα σύνολα ειδικών λύσεων είναι, μέσω της f = -g, ένα-προς-ένα F <-> G, ας παρατηρήσουμε πως στην ίδια αρχική συνθήκη (0, 1) αντιστοιχεί η σταθερά C1 = 1 της πρώτης ΔΕ και η σταθερά C2 = -1 της δεύτερης ΔΕ, δηλαδή C1 =/= C2, δηλαδή πως η σταθερά C εξαρτάται εκτός από την αρχική συνθήκη ΚΑΙ από τον τύπο της οικογένειας των ειδικών λύσεων στις οποίες μετέχει.
= Ε, και;
- Να! Για την ίδια αρχική συνθήκη, στην μοναδική ειδική λύση της πρώτης ΔΕ ("κόκκινη" καμπύλη στο δεύτερο σχήμα)- *ΔΕΝ* αντιστοιχεί, μέσω της 1 <-> 1 αντιστοιχίας g = -f, η μοναδική ειδική λύση της δεύτερης ΔΕ ("κόκκινη" καμπύλη στο τέταρτο σχήμα). Πράγματι. Για την πρώτη ΔΕ έχουμε τον τύπο μοναδικής λύσης y1 = 1/(x + C1) και C1 = 1 με μέγιστο διάστημα ορισμού γενικής αρχικής συνθήκης (-1, +οο), ενώ για την δεύτερη ΔΕ έχουμε τον τύπο μοναδικής λύσης y2 = -1/(x + C2) και C2 = -1 με μέγιστο διάστημα ορισμού γενικής αρχικής συνθήκης (-οο, 1), οπότε, οι δύο λύσεις έχουν διαφορετικό διάστημα-σύνολο ορισμού ( και με την ευκαιρία, μόνον ακριβώς ένα κοινό σημείο, το (0, 1), αφού μόνον εκεί 1/(χ + 1) = -1/(x -1) <=> 2x = 0 <=> x = 0 <=> 1/1 = -1/(-1) ), άρα, αφού η αντίθετη της πρώτης y1 έχει το ίδιο διάστημα-σύνολο ορισμού με την y1, η -y1 έχει διαφορετικό διάστημα-σύνολο ορισμού από την y2 και έτσι είναι διαφορετική από την y2. Μια τελευταία ματιά στους διαφορετικούς τύπους: -y1 = -1/(x + 1) και y2 = -1/(x - 1), καθώς και στην τιμή του πρώτου στο χ0 = 0, που δίνει -y1(x0=0) = -1, και η διαφορά μεταξύ τους ελπίζω πως εμπεδώνεται οριστικά.
- Πέτρος Ζιμουρτόπουλος

