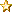1ο ερώτημαΈστω ο τριδιαγώνιος πίνακας
Α (πάντα τετραγωνικός):
$\[A_{n,n} = \begin{pmatrix}
a_{1,1} & a_{1,2} & 0 & 0 & \cdots & 0 \\
a_{2,1} & a_{2,2} & a_{2,3} & 0 & \cdots & 0 \\
0 & a_{3,2} & a_{3,3} & a_{3,4} & \cdots & 0 \\
\vdots & & & \ddots & \vdots \\
0 & \cdots & 0 & a_{n,n-1} & a_{n,n}
\end{pmatrix}
\]$
και
έστω το διάνυσμα
χ:
$\[\vec{x_{n}} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{pmatrix}\]$
Το γινόμενό τους έστω
u είναι ένα n-διάστατο διάνυσμα της μορφής:
$\[\vec{u_{n}} = \begin{pmatrix}
a_{1,1} \cdot x_1 + a_{1,2} \cdot x_2 + 0 \\
a_{2,1} \cdot x_1 + a_{2,2} \cdot x_2 + a_{2,3} \cdot x_3 \\
a_{3,2} \cdot x_2 + a_{3,3} \cdot x_3 + a_{3,4} \cdot x_4 \\
\vdots \\
0 + a_{n,n-1} \cdot x_{n-1} + a_{n,n} \cdot x_n\\
\end{pmatrix}\]$
Όπως βλέπεις στο διάνυσμα του γινομένου, έχεις άθροισμα τριάδων. Για να το προγραμματίσεις θα χρειαστείς έναν μετρητή (έστω j) που θα μεταβάλλεται από 1 έως n.
Κάθε συντεταγμένη του γινομένου σχηματίζεται από τον εξής τύπο: u[j] = a[j,j-1]*x[j-1] + a[j,j]*x[j] + a[j,j+1]*x[j+1]
Προσοχή! για j=1 και j=n (πρώτη και τελευταία γραμμή) βγαίνουμε εκτός των ορίων του πίνακα (0 και n+1) άρα πρέπει να τα "μηδενίσεις".
Θα κάνουμε επαλήθευση στο παραπάνω τύπο, για να δούμε αν θα μας δώσει τα στοιχεία που βγάλαμε παραπάνω:
j=1: u[1] =
a[1,0]*x[0] + a[1,1]*x[1] + a[1,2]*x[2] =
a[1,1]*x[1] + a[1,2]*x[2]j=2: u[2] =
a[2,1]*x[1] + a[2,2]*x[2] + a[2,3]*x[3]...
j=n: u[n] = a[n,n-1]*x[n-1] + a[n,n]*x[n] +
a[n,n+1]*x[n+1] =
a[n,n-1]*x[n-1] + a[n,n]*x[n]Άρα τώρα μπορούμε να αρχίσουμε να προγραμματίζουμε...
*Σημείωση: Ίσως έκανα υπερβολική ανάλυση του προβλήματος. Στόχος μου, όμως, είναι να δείξω σε εσένα (και κάθε άλλο τυχόν μελλοντικό αναγνώστη του forum) βήμα-βήμα τη διαδικασία με την οποία πρέπει να σκεφτόμαστε για να αναγάγουμε ένα (πολύ απλό στη συγκεκριμένη περίπτωση) μαθηματικό πρόβλημα σε αλγόριθμο, ώστε στη συνέχεια να μπορέσουμε να το προγραμματίσουμε.
**Κώδικας σε LaTeX που χρησιμοποιήθηκε για την αναπαράσταση των πινάκων και διανυσμάτων:
- Κώδικας: Επιλογή όλων
[tex]\[A_{n,n} = \begin{pmatrix}
a_{1,1} & a_{1,2} & 0 & 0 & \cdots & 0 \\
a_{2,1} & a_{2,2} & a_{2,3} & 0 & \cdots & 0 \\
0 & a_{3,2} & a_{3,3} & a_{3,4} & \cdots & 0 \\
\vdots &&& \ddots & \vdots \\
0 & \cdots & 0 & a_{n,n-1} & a_{n,n}
\end{pmatrix}\][/tex]
[tex]\[\vec{x_{n}} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{pmatrix}\][/tex]
[tex]\[\vec{u_{n}} = \begin{pmatrix}
a_{1,1} \cdot x_1 + a_{1,2} \cdot x_2 + 0 \\
a_{2,1} \cdot x_1 + a_{2,2} \cdot x_2 + a_{2,3} \cdot x_3 \\
a_{3,2} \cdot x_2 + a_{3,3} \cdot x_3 + a_{3,4} \cdot x_4 \\
\vdots \\
0 + a_{n,n-1} \cdot x_{n-1} + a_{n,n} \cdot x_n\\
\end{pmatrix}\][/tex]
Τσορμπατζόγλου.Γιώργος
Μπορεί κάποιος να εξηγησει πώς λειτουργεί το split και η σύνταξη του?
