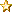Χμμμ αρκετά ζόρικο το 2ο ολοκλήρωμα. Έπρεπε να παρατηρήσεις ότι στο παρονομαστή έχεις (1+χ²) το οποίο είναι η παράγωγός του Arctanx άρα να γράψεις τη παράσταση του ολοκληρώματος ως: $\frac{1}{2}(\frac{x}{1+x^2})^2dArctan^2x$ να εκτελέσεις την αντικατάσταση Arctan²x=u <=> x=sqrt(tanu) οπότε ανάγεται σε τριγωνομετρικό το οποίο λύνεις με τις γνωστές αντικαταστάσεις του τυπολογίου. [Σημείωση: Arctan(inf) = π/2]
Δε ξέρω αν κανένας το έλυσε με πιο εύκολο τρόπο ή έχει κανένα άλλο κόλπο... Έχει καιρό που πέρασα το μάθημα
από iakovos » 19 Φεβ 2009, 13:39 
themata anal1.pdf
